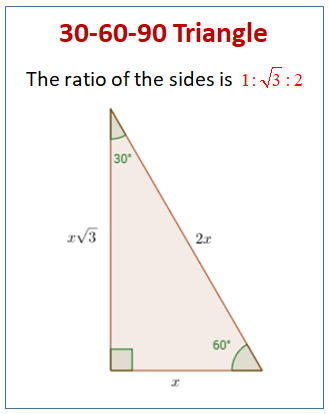
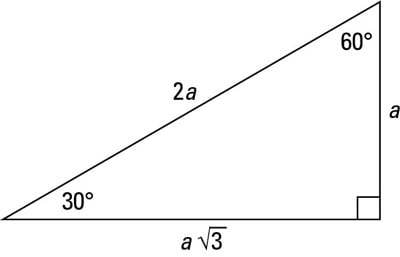
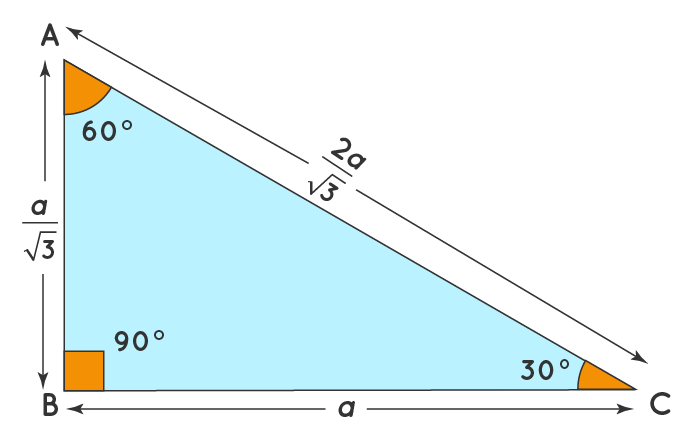
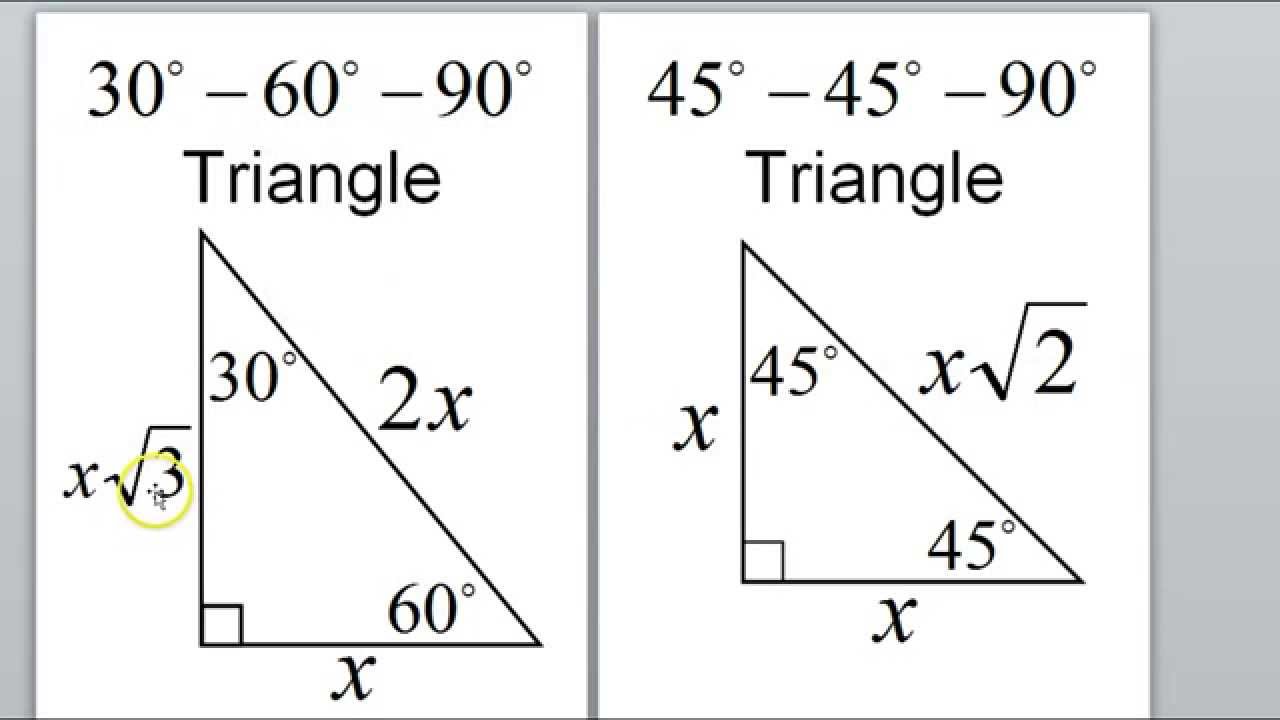
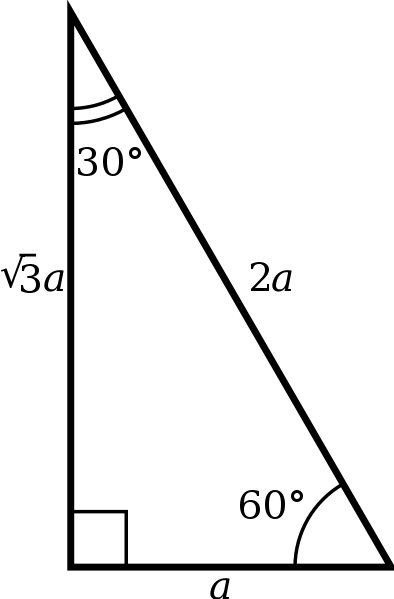
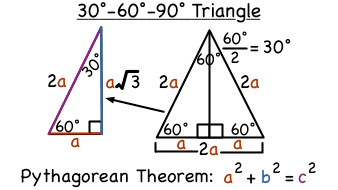
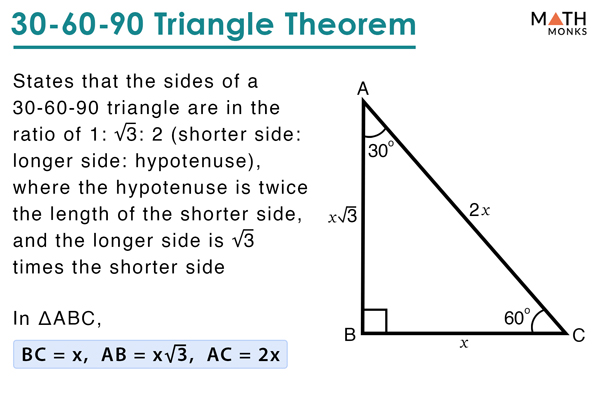
Y√3 = Long side (opposite the 60° angle) These three special rules can be considered the triangle theorem and are unique to these special right triangles The hypotenuse (the triangle's longest side) is always twice the length of the short leg The length of the longer leg is the short leg's length times √3 Triangle Practice Name_____ ID 1 Date_____ Period____ ©v j2o0c1x5w UKVuVt_at iSGoMfttwPaHrGex rLpLeCkQ l ^AullN Zr\iSgqhotksV vrOeXsWesrWvKe`d\1Find the missing side lengths Leave your answers as radicals in simplest form 1) 12 m n 30° 2) 72 ba 30° 3) x y 5 60° 4) x 133y 60° 5) 23 u v 60° 6) m n63Special Right Triangles inA right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1 √3 3 2 That is to say, the hypotenuse is twice as long as the shorter leg, andA 30̊ 60̊ 90̊ right triangle or

30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com
What is the 30 60 90 triangle formula
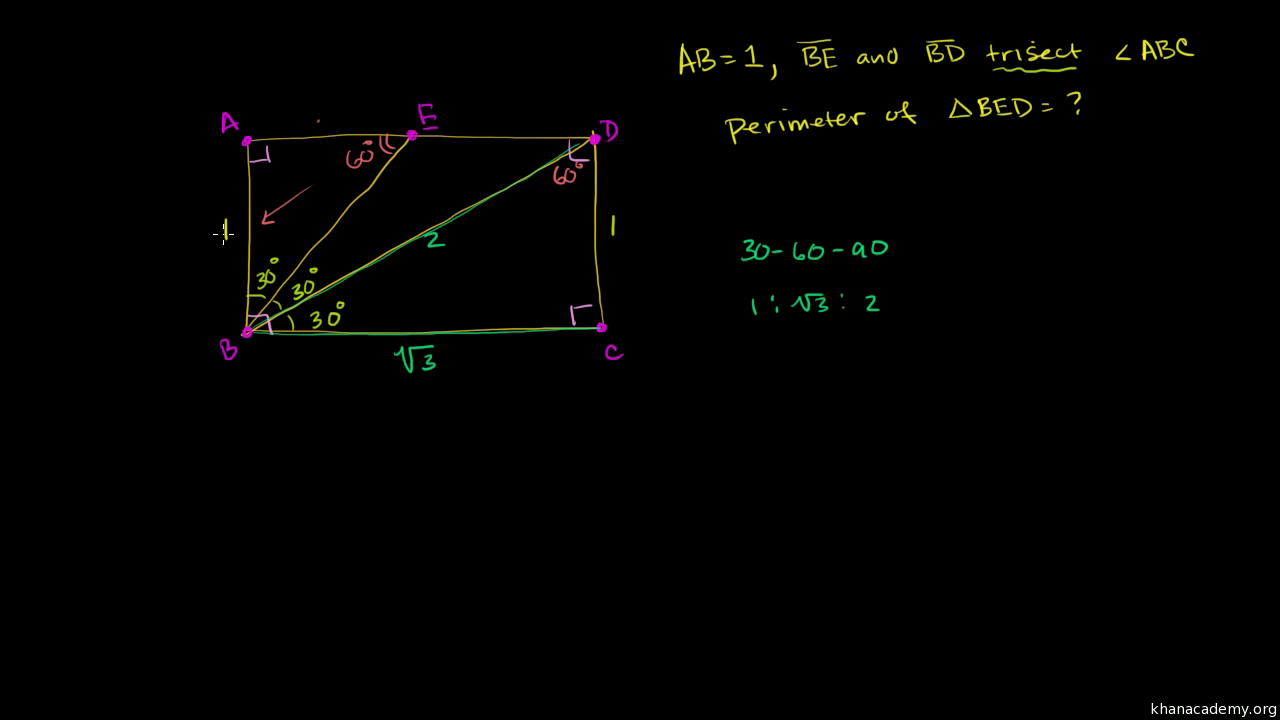
What is the 30 60 90 triangle formula-Definitions and formulas for the area of a triangle, the sum of the angles of a triangle, the Pythagorean theorem, Pythagorean triples and special triangles (the triangle and the triangle) Just scroll down or click on what you want and I'll scroll down for you!Triangle example problem Our mission is to provide a free, worldclass education to anyone, anywhere Khan Academy is a 501(c)(3) nonprofit organization



30 60 90 Triangle Rules
30 60 90 triangle rules and properties The most important rule to remember is that this special right triangle has one right angle and its sides are in an easytoremember consistent relationship with one another the ratio is a a√3 2a A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another8 rows Example 1 Find the length of the hypotenuse of a rightangle triangle if the other two sides
This means that This means that the sine and cosine of 45° are equal to , which is equal to Since the cotangent can be defined as the cosine divided by the sine, the cotangent of 45° is equal to 1 We can find the cotangent of 30° and 60° using the special triangle 30°60°90° This triangle has sides of ratio 1 2Special right triangles hold many applications in both geometry and trigonometry In this lesson you will learn the general formula for the ratios, and how to find missing sides of any 30 60 90 right triangle A triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle) Because the angles are always in that ratio, the sides are also always in the same ratio to each other The side opposite the 30º angle is the shortest and the length of it is usually labeled as x The side opposite the 60º angle has a
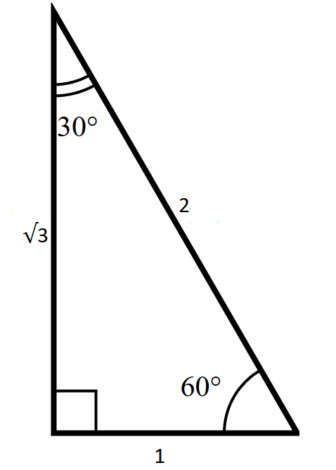
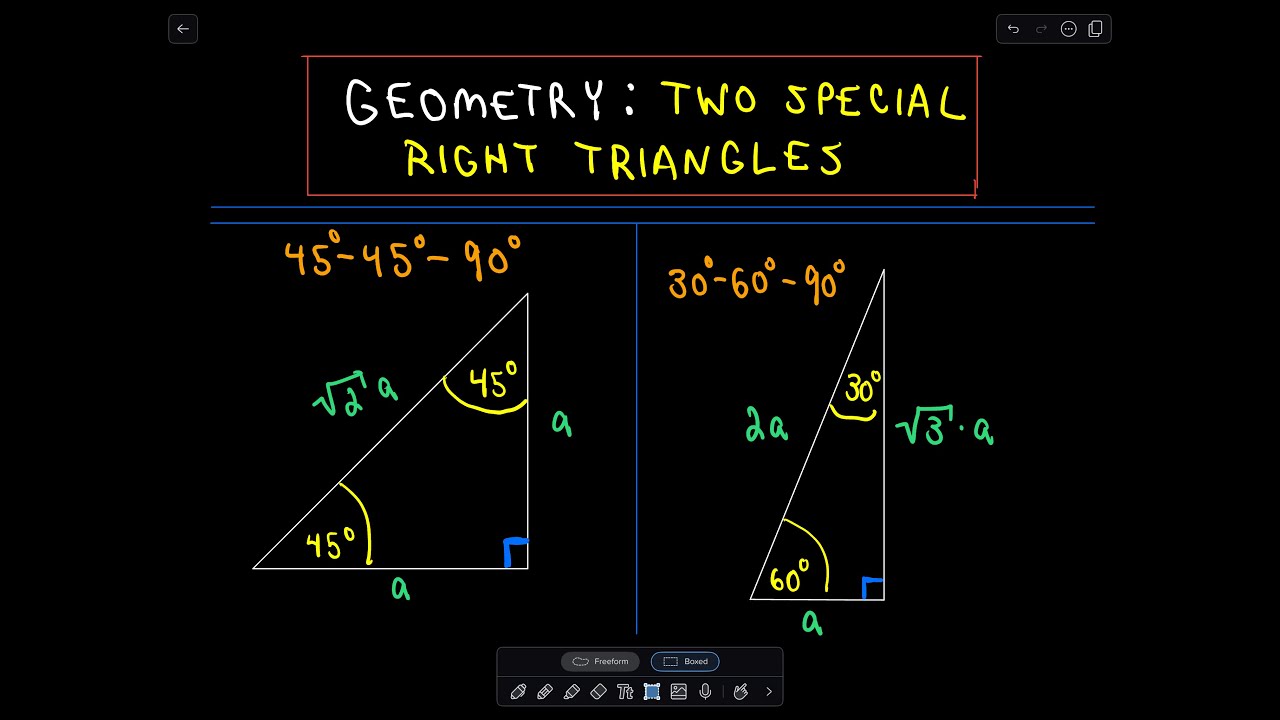
The ratio of the sides follow the triangle ratio 1 2 √3 1 2 3 Short side (opposite the 30 30 degree angle) = x x Hypotenuse (opposite the 90 90 degree angle) = 2x 2 x Long side (opposite the 60 60 degree angle) = x√3 x 3Triangles are explained in this step by step example To see all my videos visit http//MathMeetingcom= nn√32n Step 2 Yes, it is a triangle with n = 4



30 60 90 Special Right Triangles Videos Worksheets Examples Solutions




30 60 90 Triangle Theorem Ratio Formula Video
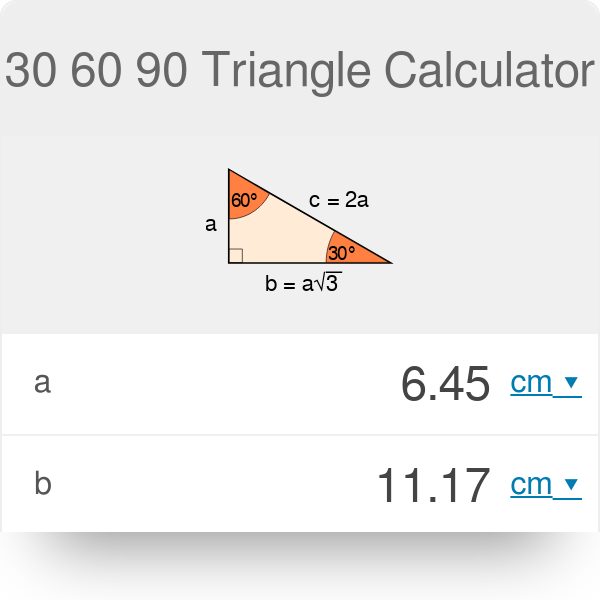
Multiply this answer by the square root of 3 to find the long leg Type 3 You know the long leg (the side across from the 60degree angle) Divide this side by the square root of 3 to find the short side Double that figure to find the hypotenuse Finding the other sides of a triangle when you know the hypotenuseUsing what we know about triangles to solve what at first seems to be a challenging problem Created by Sal Khan Special right triangles Special right triangles proof (part 1) Special right triangles proof (part 2) Practice Special right triangles triangle example problem This is the currently selected item Thanks to this 30 60 90 triangle calculator you find out that shorter leg is 635 in because a = b√3/3 = 11in * √3/3 ~ 635 in hypotenuse is equal to 127 in because c = 2b√3/3 = 2a ~ 127 in area is 349 in² it's the result of multiplying the legs length and dividing by




30 60 90 Triangle Calculator Formula Rules



45 45 90 Triangle Explanation Examples
Special triangles – Formula and examples Special triangles are right triangles that have special proportions for their sides The 30°60°90° triangle has the proportions 1√32 The 45°45°90° triangle has the proportions 11√2 All the lengths of these sides can be easily found if we only know the length of one of the sides A right triangle is a special type of right triangle 30 60 90 triangle's three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1√ (3/2) This means that the hypotenuse is twice as long as the shorter leg and the longer leg is the square root ofThe right triangle is a special case triangle, with angles measuring 30, 60, and 90 degrees This free geometry lesson introduces the subject and provides examples for calculating the lengths of sides of a triangle



The 30 60 90 Triangle Topics In Trigonometry



The Easy Guide To The 30 60 90 Triangle
Qualities of a Triangle A triangle is special because of the relationship of its sides Hopefully, you remember that the hypotenuse in a right triangle is the longest side Qualities of a Triangle A triangle is special because of the relationship of its sides Hopefully, you remember that the hypotenuse in a right triangle is the longest side, which is also directly across from the 90 degree angle It turns out that in a triangle, you can find the measure of any of the three sides, simply by knowing the measure Example 1 We can see that this is a right triangle in which the hypotenuse is twice the length of one of the legs This means this must be a triangle and the smaller given side is opposite the 30° The longer leg must, therefore, be opposite the 60° angle and measure 6 *



30 60 90 Triangle Formulas Rules And Sides Science Trends



High School Geometry Common Core G Srt B 5 Geometric Mean Special Right Triangles Teacher Notes Patterson
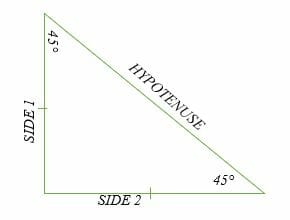
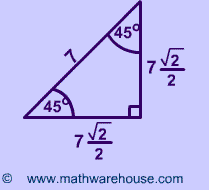
The 45°45°90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45°45°90°, follow a ratio of 11√ 2 Like the 30°60°90° triangle, knowing one side length allows you to determine the lengths of the other sidesRelated Pages Right Triangle Other Special Right Triangles More Geometry Lessons Recognizing special right triangles in geometry can provide a shortcut when answering some questions A special right triangle is a right triangle whose sides are in a particular ratioYou can also use the Pythagorean theorem formula, but if you can see that it is a special triangle it canA triangle is a right triangle with angle measures of 30º, 60º



Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
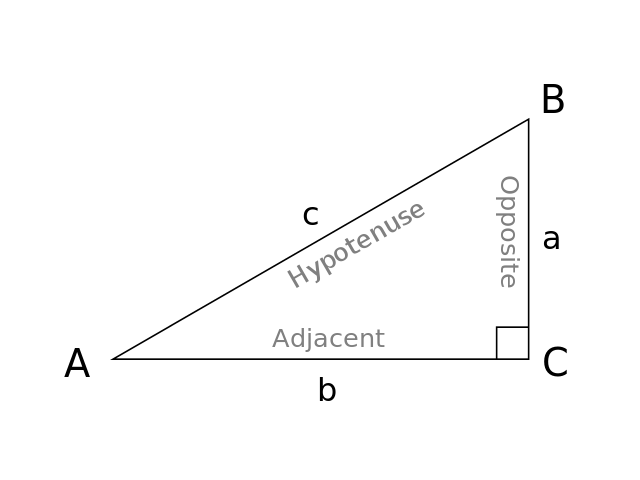
For any problem involving a 30°60°90° triangle, the student should not use a table The student should sketch the triangle and place the ratio numbers Since the cosine is the ratio of the adjacent side to the hypotenuse, you can see that cos 60° = ½ Example 2 Evaluate sin 30° Answer According to the property of cofunctions (Topic 3), sin 30° is equal to cos 60° sin 30° = ½Right triangle calculator, 30 60 90 formula, 45 triangle, special area, unit circle calculator There are two of them 30 60 90 and 45 45 90 The ratio of the first is {eq}1 \sqrt {3} 2 {/eq} and the ratio of the second is {eq}1 1 \sqrt {2} {/eq} The first ratio means that



A Quick Guide To The 30 60 90 Degree Triangle Dummies



30 60 90 Triangle Definition Theorem Formula Examples
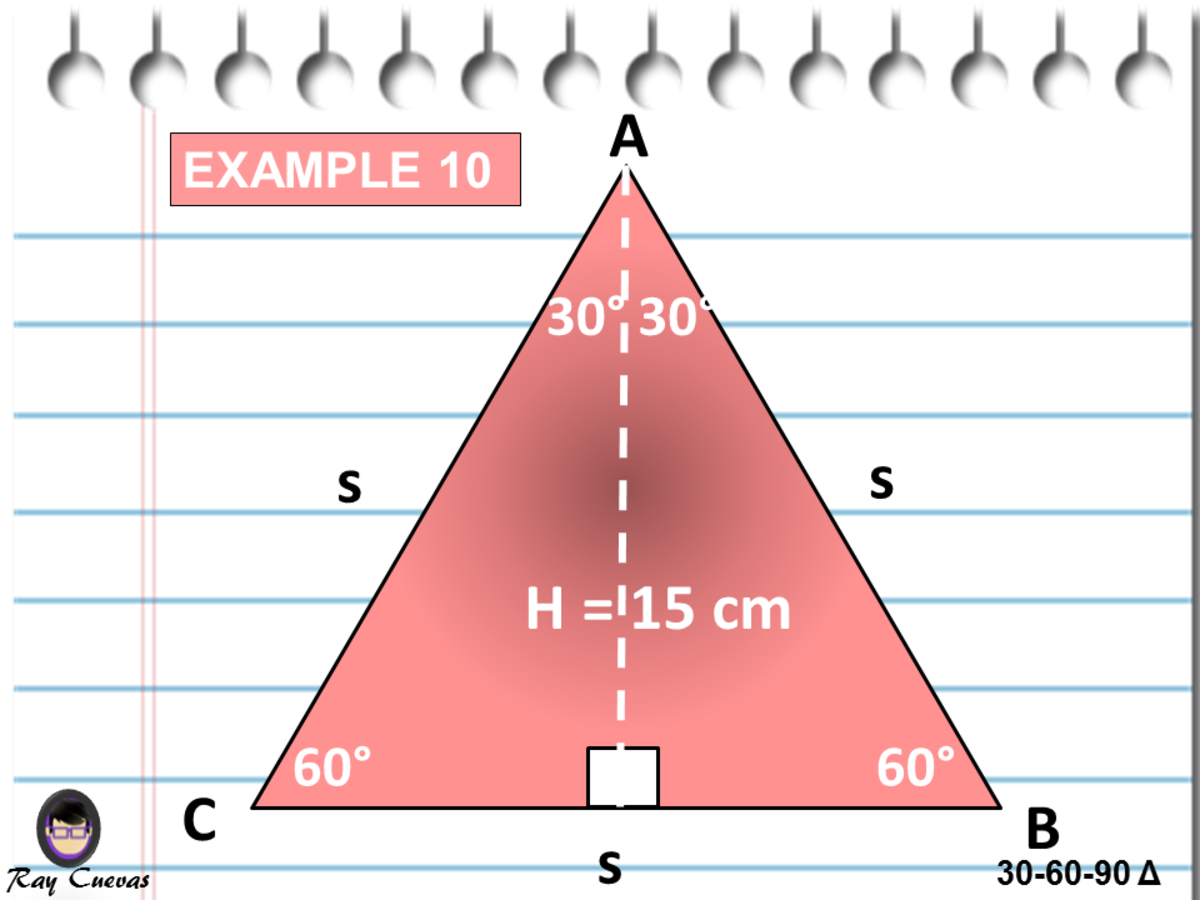
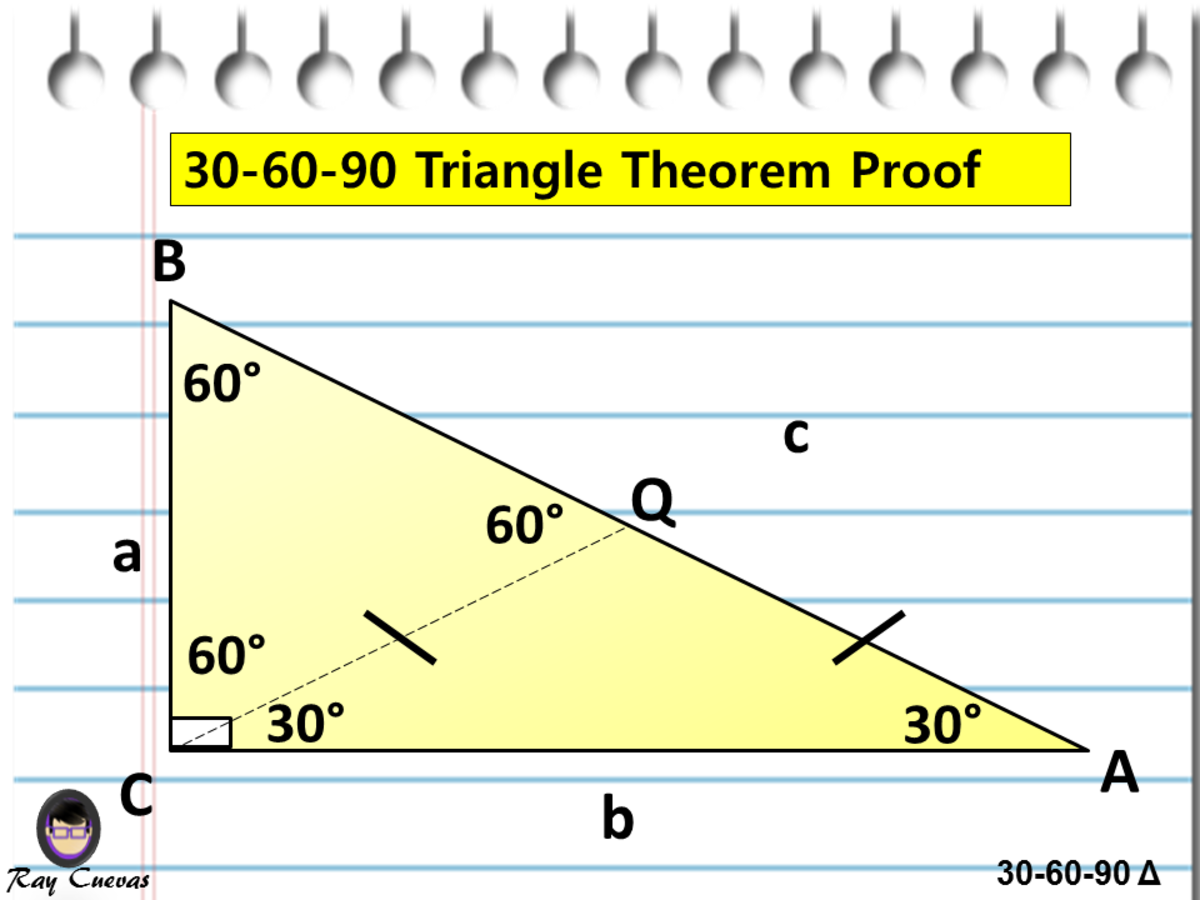
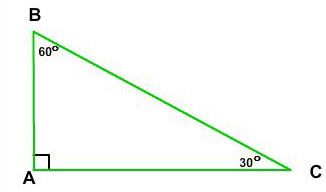
The sides of a right triangle lie in the ratio 1√32 The side lengths and angle measurements of a right triangle Credit Public Domain We can see why these relations should hold by plugging in the above values into the Pythagorean theorem a2 b2 = c2 a2 ( a √3) 2 = (2 a) 2 a2 3 a2 = 4 a2A 30 60 90 triangle completes an arithmetic progression 3030=6030 =90 An arithmetic progression is a sequence of numbers in which the difference of any two successive numbers is a constant For instance, 2,4,6,8 is an arithmetic progression with a constant of 2Example 1 Find the missing side of the given triangle Solution As it is a right triangle in which the hypotenuse is the double of one of the sides of the triangle Thus, it is called a triangle where smaller angle will be 30 The longer side is always opposite to 60° and the missing side measures 3√3 units in the given figure




Special Right Triangles 45 45 30 60 90 Notes Sheet Graphic Organizers



The Easy Guide To The 30 60 90 Triangle
The reason these triangles are considered special is because of the ratios of their sides they are always the same!Although all right triangles have special features – trigonometric functions and the Pythagorean theoremThe most frequently studied right triangles, the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 trianglesThe 30–60–90 Day Plan is a document prepared by a job seeker and presented during an interview It is an outline of what the candidate intends or proposes to achieve in the first 90 days, if hired for the role Beside above, what are the sides of a 30 60 90 Triangle?



30 60 90 Triangle Rules



Day 1 Hw Special Right Triangles 45 45 90 30 60 90 Youtube
Because a right triangle has to have one 90° angle by definition and the other two angles must add up to 90° So $90/2 = 45$) Triangles A triangle is a special right triangle defined by its angles It is a right triangle due to its 90° angle, and the other two angles must be 30° and 60° 345, and Right A triangle is a right triangle with angles 30^@, 60^@, and 90^@ and which has the useful property of having easily calculable side lengths without use of trigonometric functions A triangle is a special right triangle, so named for the measure of its angles Its side lengths may be derived in the following mannerSpecial Right Triangle Formulas Learn Formulas Related 7 hours ago Cuemathcom Visit Site Examples Using Special Right Triangle FormulaExample 1 Find the other two sides of the rightangled triangle if the base of the triangle is 5√3 and angles measure 30, 60, and 90 degrees Solution To find Length of the sides of the triangleBase = 5√3 (given) Using special right



30 60 90 Triangle Formulas Rules And Sides Science Trends



30 60 90 Triangle Formulas Rules And Sides Science Trends
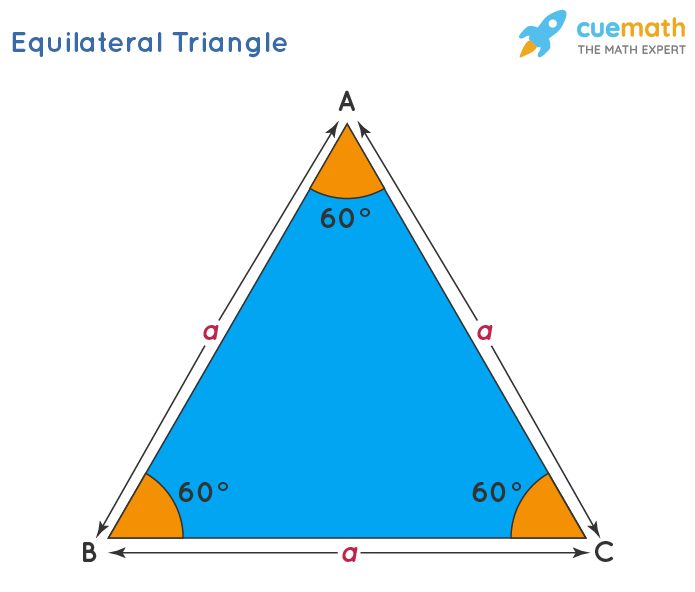
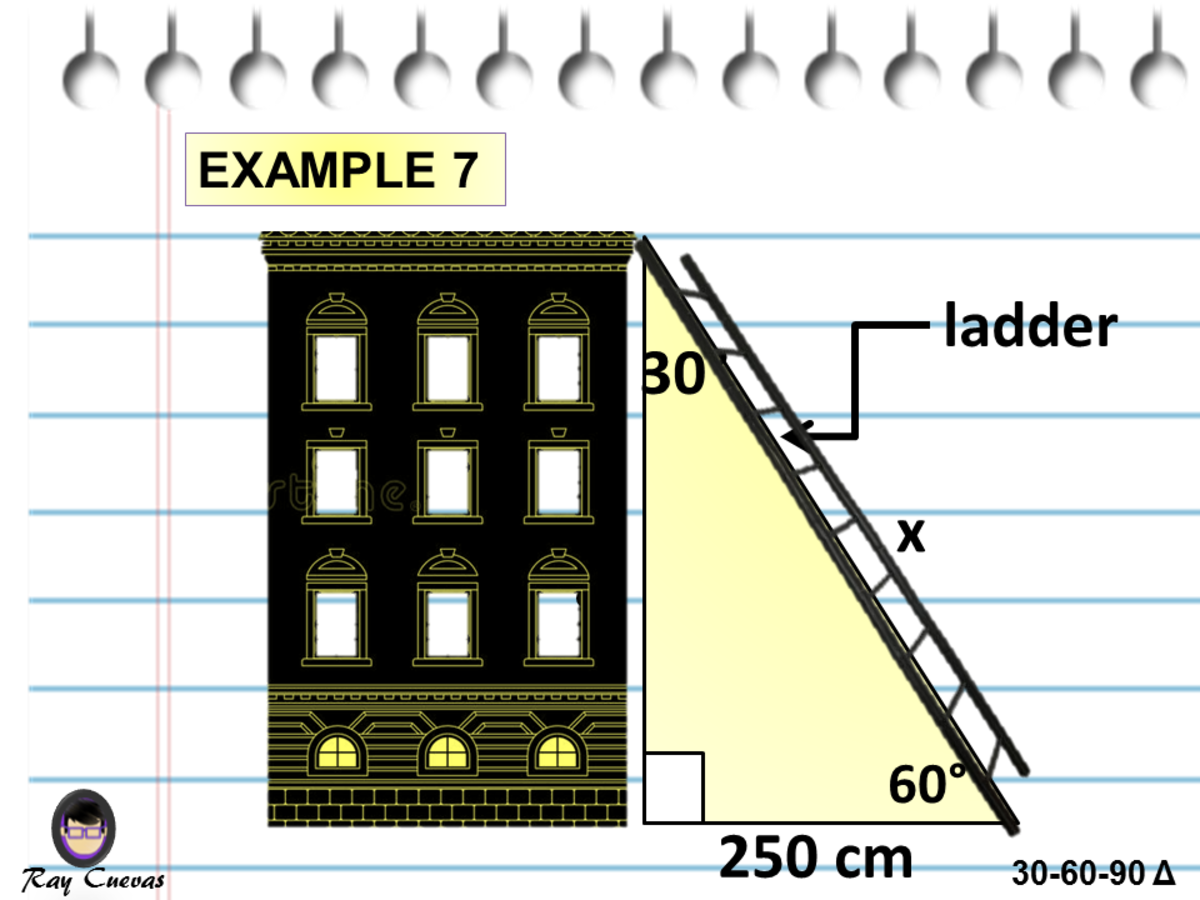
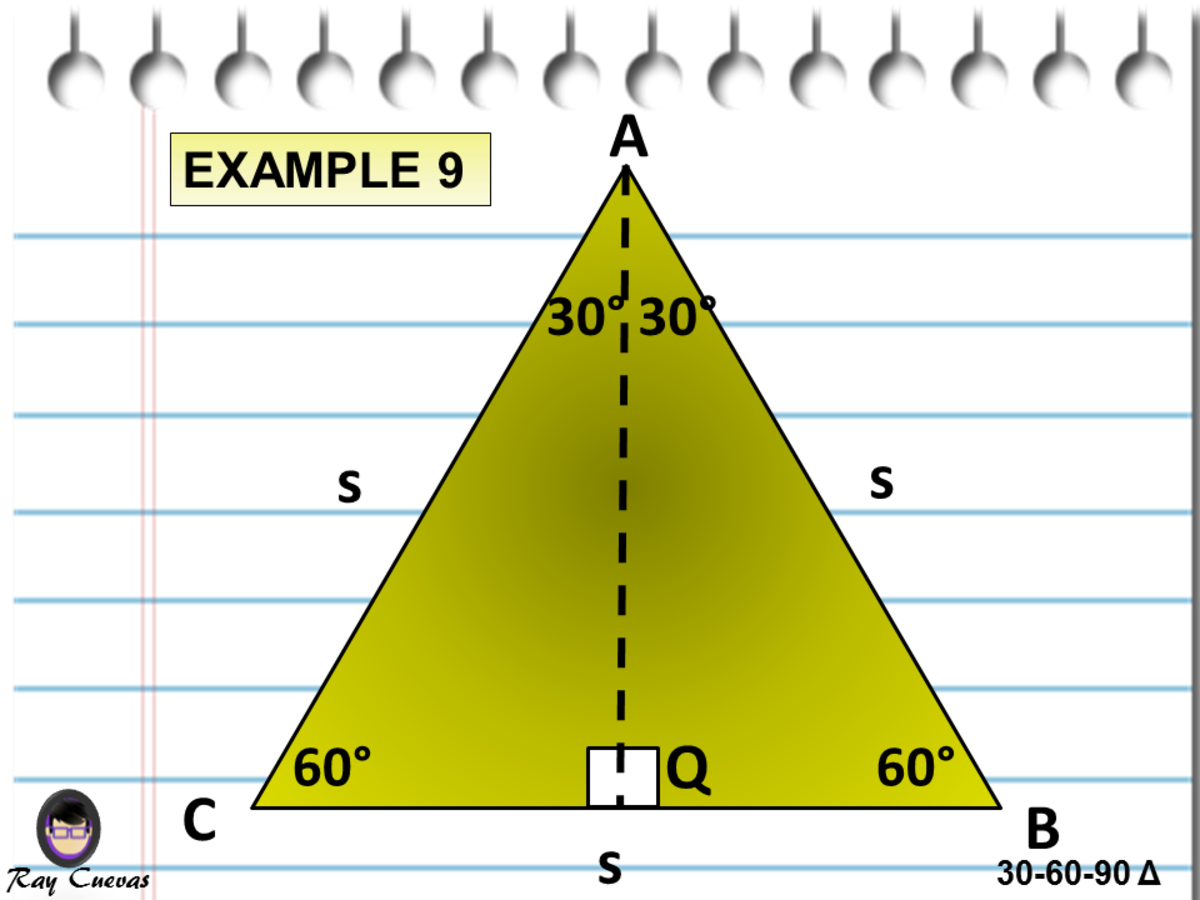
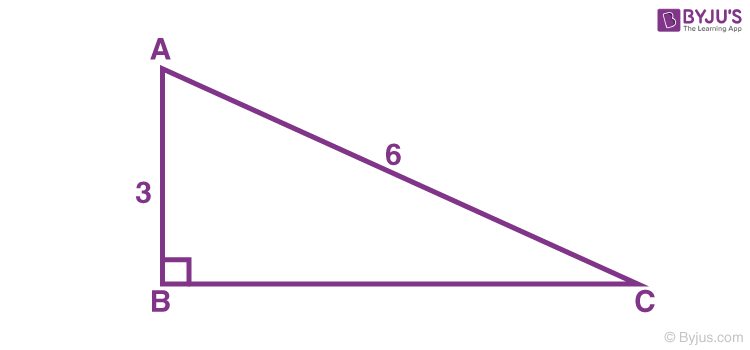
Solve problems involving right triangles Example 1 Find the length of the hypotenuse of a right triangle if the lengths of the other two sides are 4 inches and 4√3 inches Solution Step 1 Test the ratio of the lengths to see if it fits the nn√32n ratio 44√3?To learn more about Triangles enrol in our full course now https//bitly/Triangles_DMIn this video, we will learn 000 triangle017 proof of 306A triangle is a special right triangle that contains internal angles of 30, 60, and 90 degrees Once we identify a triangle to be a 30 60 90 triangle, the values of all angles and sides can be quickly identified Imagine cutting an equilateral triangle vertically, right down the middle Each half has now become a 30 60 90 triangle



1




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com



30 60 90 Triangle Definition Theorem Formula Examples
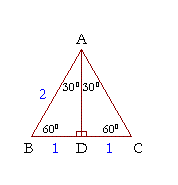



The 30 60 90 Triangle Topics In Trigonometry
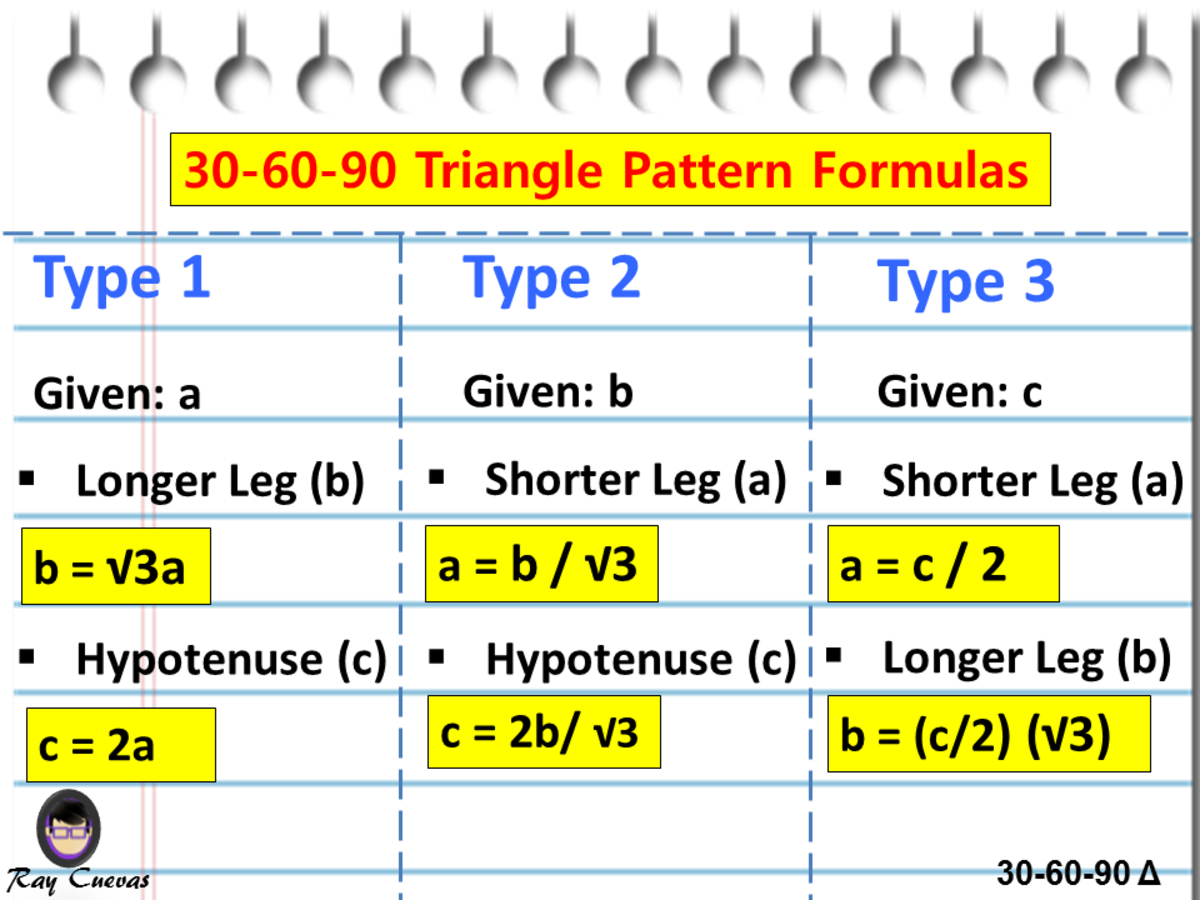



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Theorem Ratio Formula Video



30 60 90 And 45 45 90 Triangle Calculator




30 60 90 Triangle Theorem Proof Don T Memorise Youtube




30 60 90 Triangle Theorem Ratio Formula Video



3




30 60 90 Triangle Theorem Ratio Formula Video



Solve A 30 60 90 Triangle With Gradea
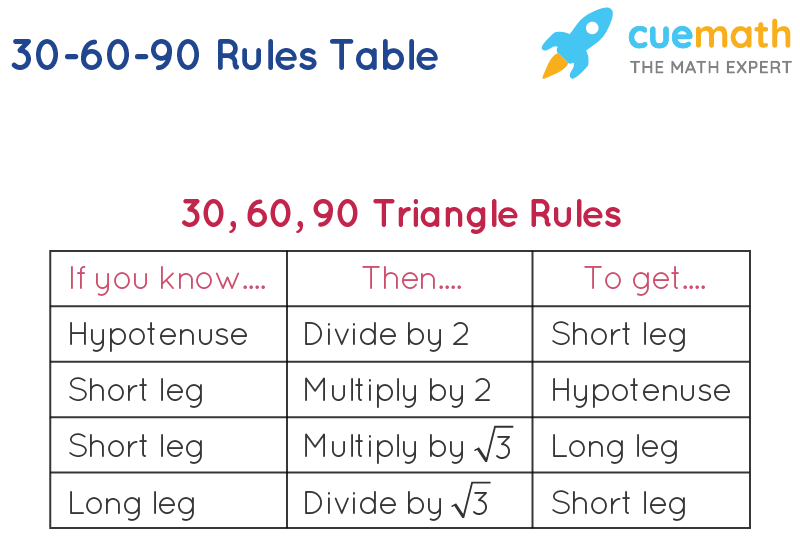



30 60 90 Formula Learn Formula For Calculating The 30 60 90 Measures
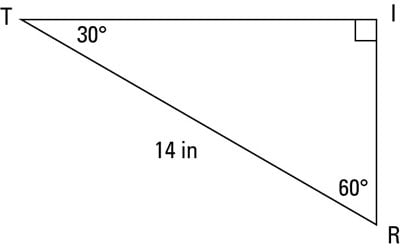



A Quick Guide To The 30 60 90 Degree Triangle Dummies




30 60 90 Triangle Theorem Ratio Formula Video




Right Triangles Interactive Notebook Pages Mrs E Teaches Math




30 60 90 Triangle Theorem Ratio Formula Video



Solve A 30 60 90 Triangle With Gradea
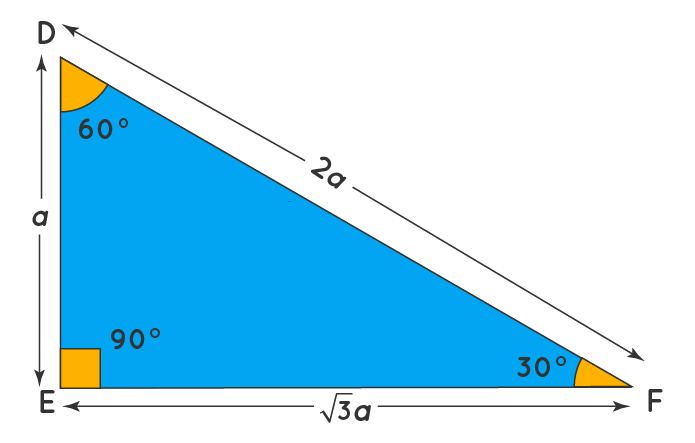



30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
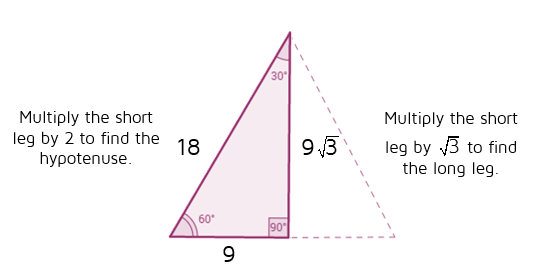



30 60 90 Triangles P4 Kate S Math Lessons
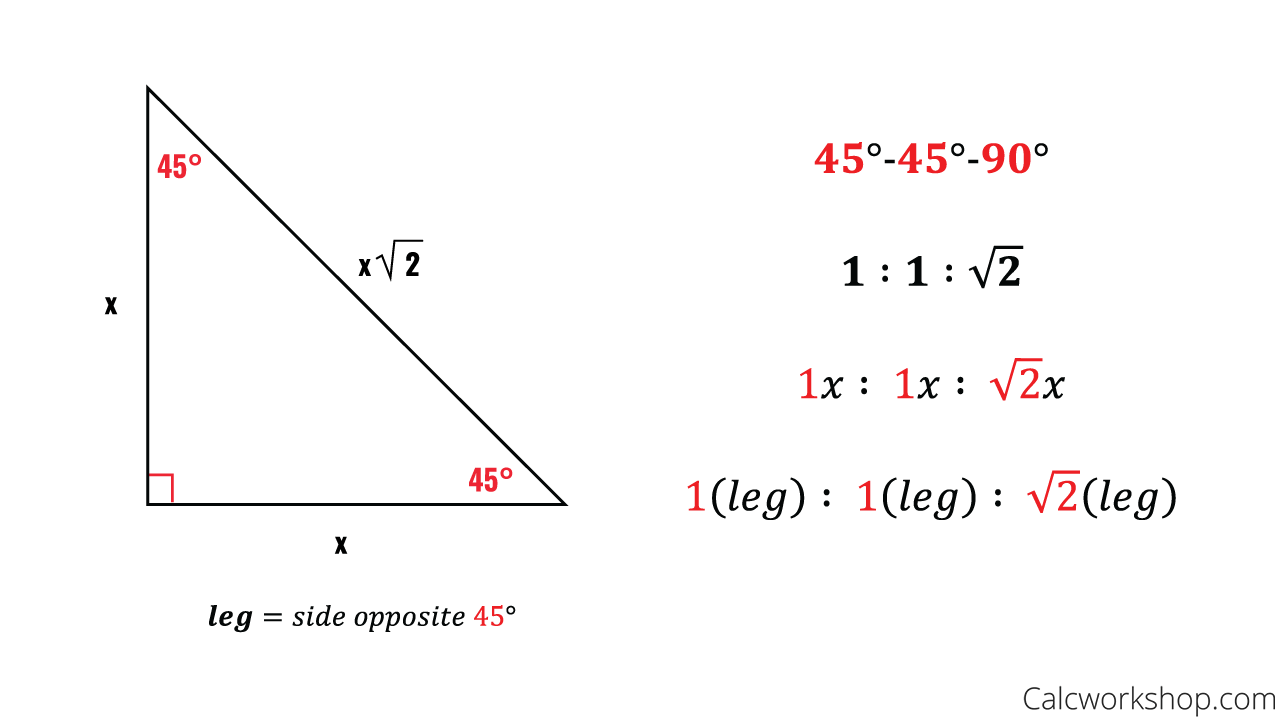



Special Right Triangles Fully Explained W 19 Examples




Right Triangles Interactive Notebook Pages Mrs E Teaches Math




30 60 90 Right Triangles Free Math Help
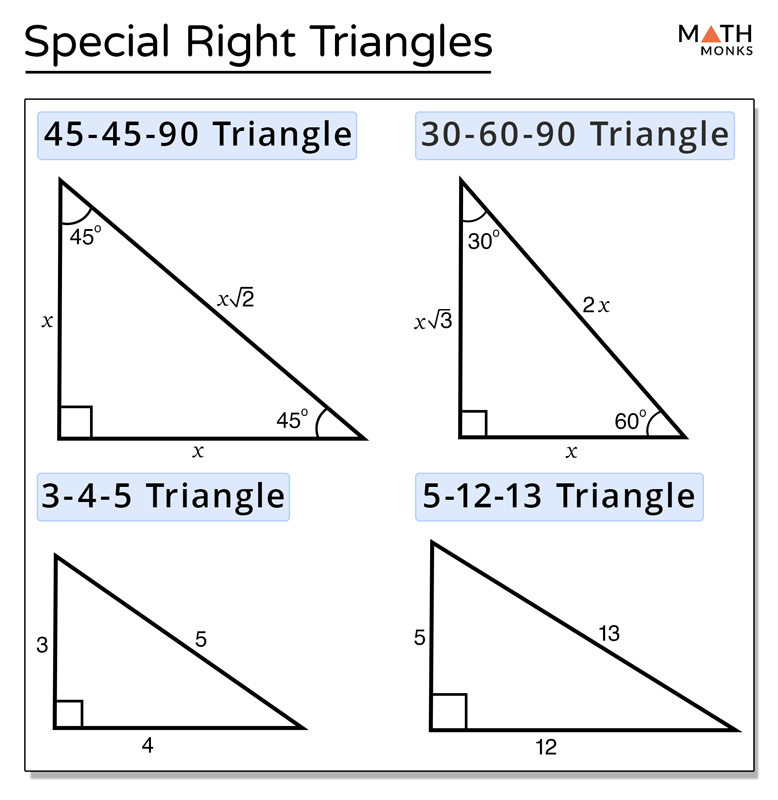



Special Right Triangles Definition Formula Examples
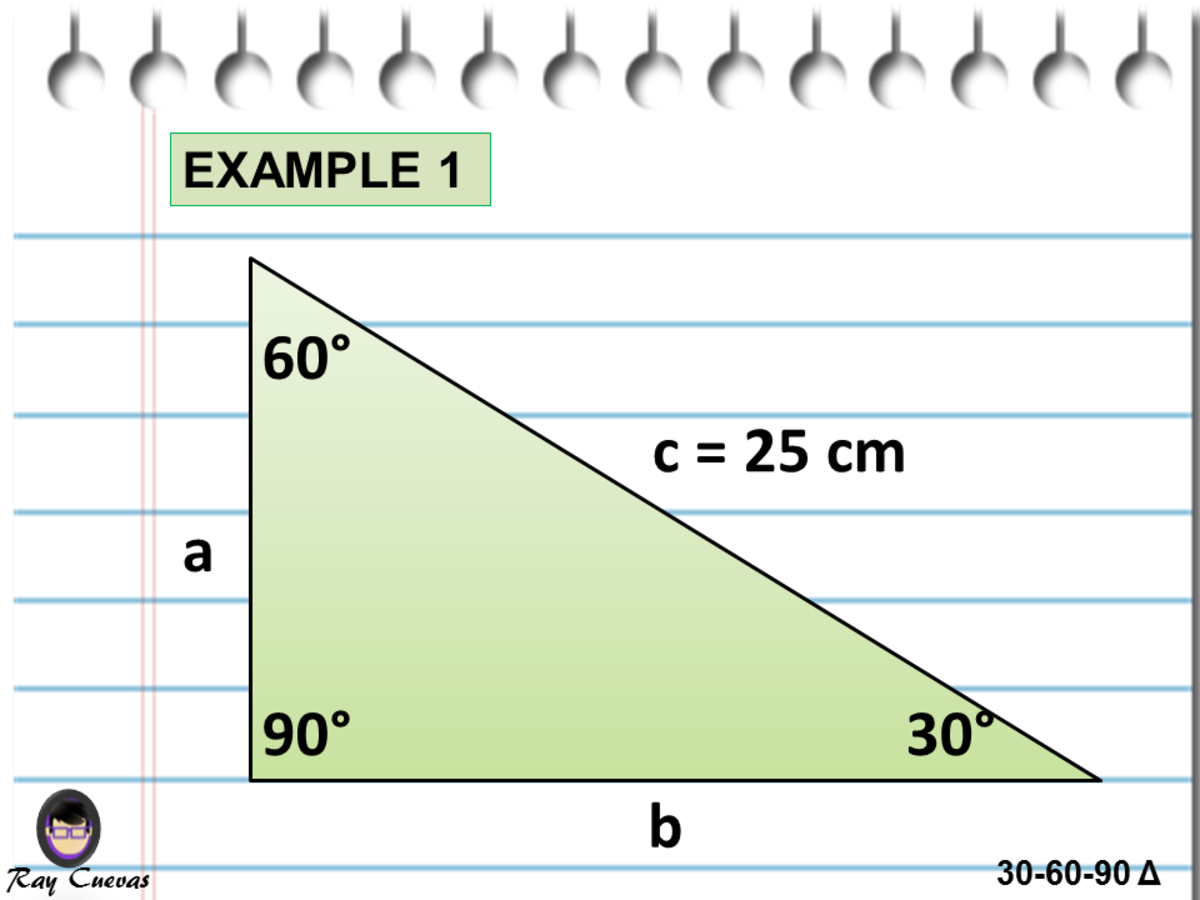



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
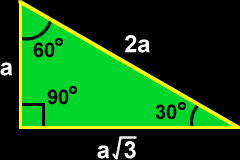



The Geometry Of Triangles
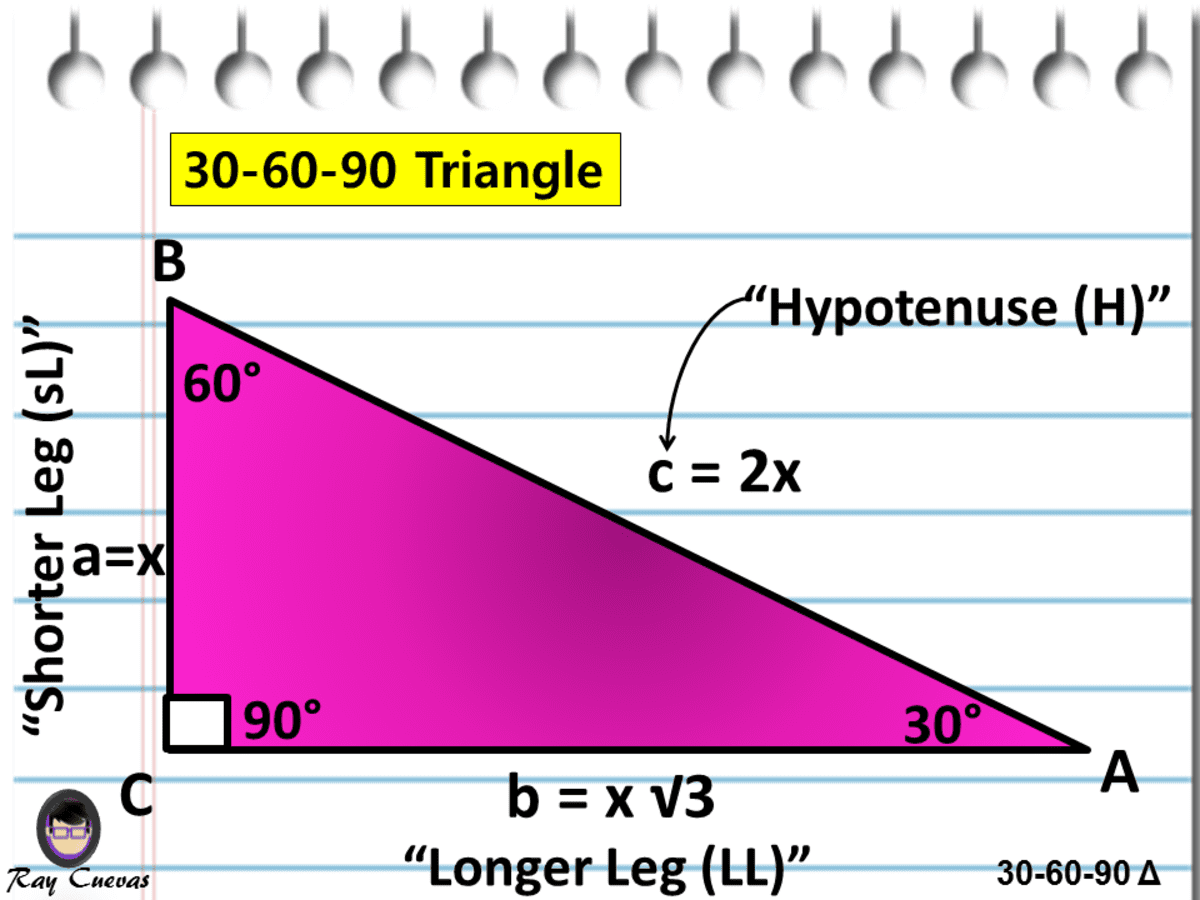



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



The Easy Guide To The 30 60 90 Triangle
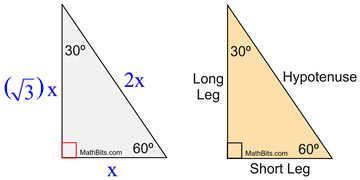



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math



Sin Cos Tan



The Complete Guide To The 30 60 90 Triangle



30 60 90 Triangle Calculator Formula Rules



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



30 60 90 Triangle Example Problem Video Khan Academy



What Is A 30 60 90 Degree Triangle Virtual Nerd



30 60 90 Triangle Definition Formulas Examples




30 60 90 Triangle Theorem Ratio Formula Video
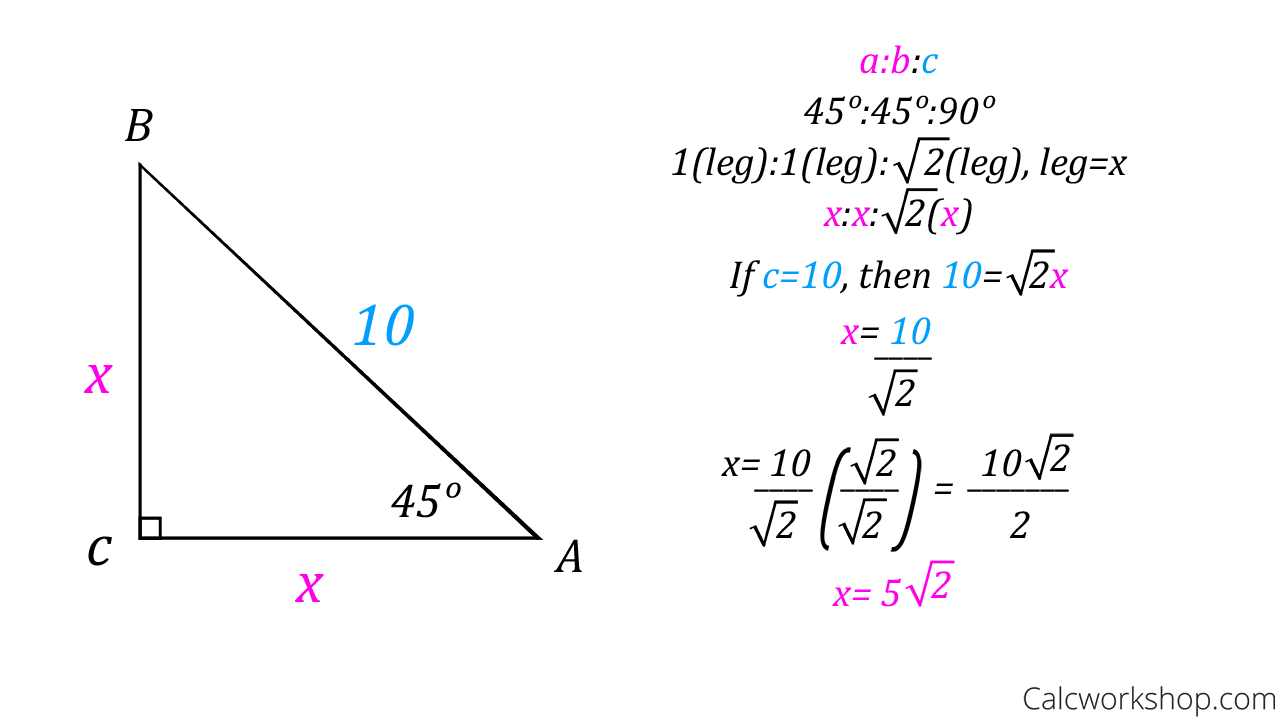



Special Right Triangles Fully Explained W 19 Examples




45 45 90 Triangle Calculator Formula Rules



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



Special Right Triangles Video Lessons Examples And Solutions




Special Right Triangles Fully Explained W 19 Examples




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



Identifying The 30 60 90 Degree Triangle Dummies
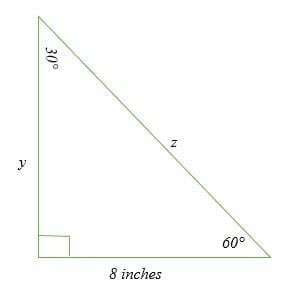



30 60 90 Triangle Explanation Examples




30 60 90 Math Methods Studying Math Physics And Mathematics
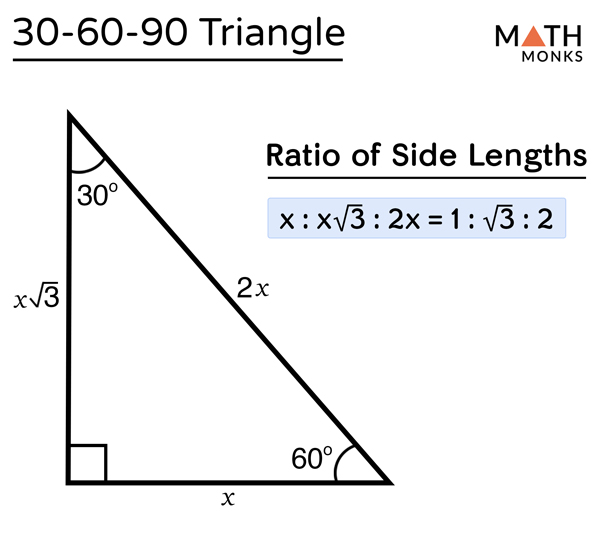



30 60 90 Triangle Definition Formulas Examples



30 60 90 Right Triangle Side Ratios Expii



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangles Hd Youtube



30 60 90 Formulas 30 60 90 Rule And Examples




30 60 90 Triangles



Special Right Triangles In Geometry 45 45 90 And 30 60 90 Youtube



The Easy Guide To The 30 60 90 Triangle



The Easy Guide To The 30 60 90 Triangle




Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
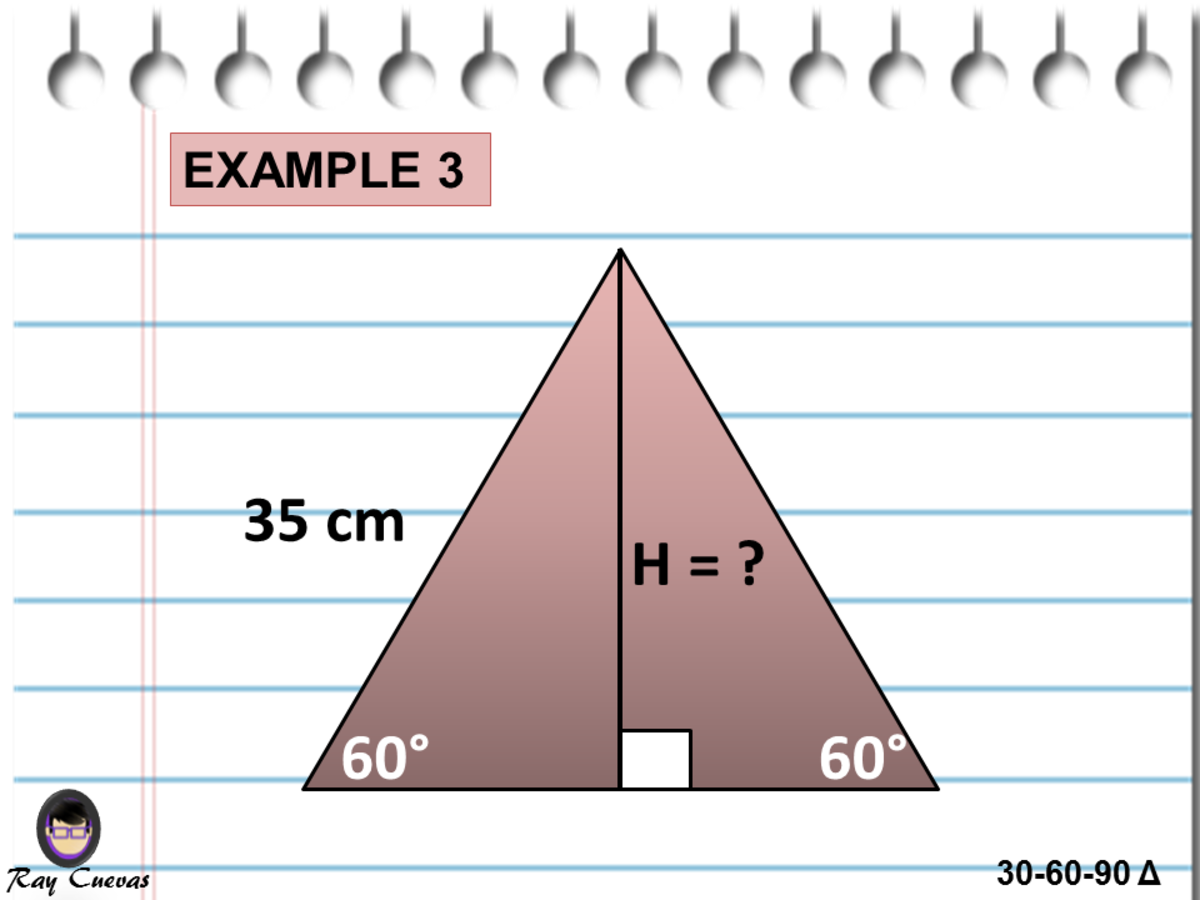



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
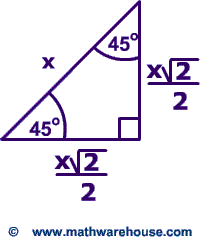



Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems
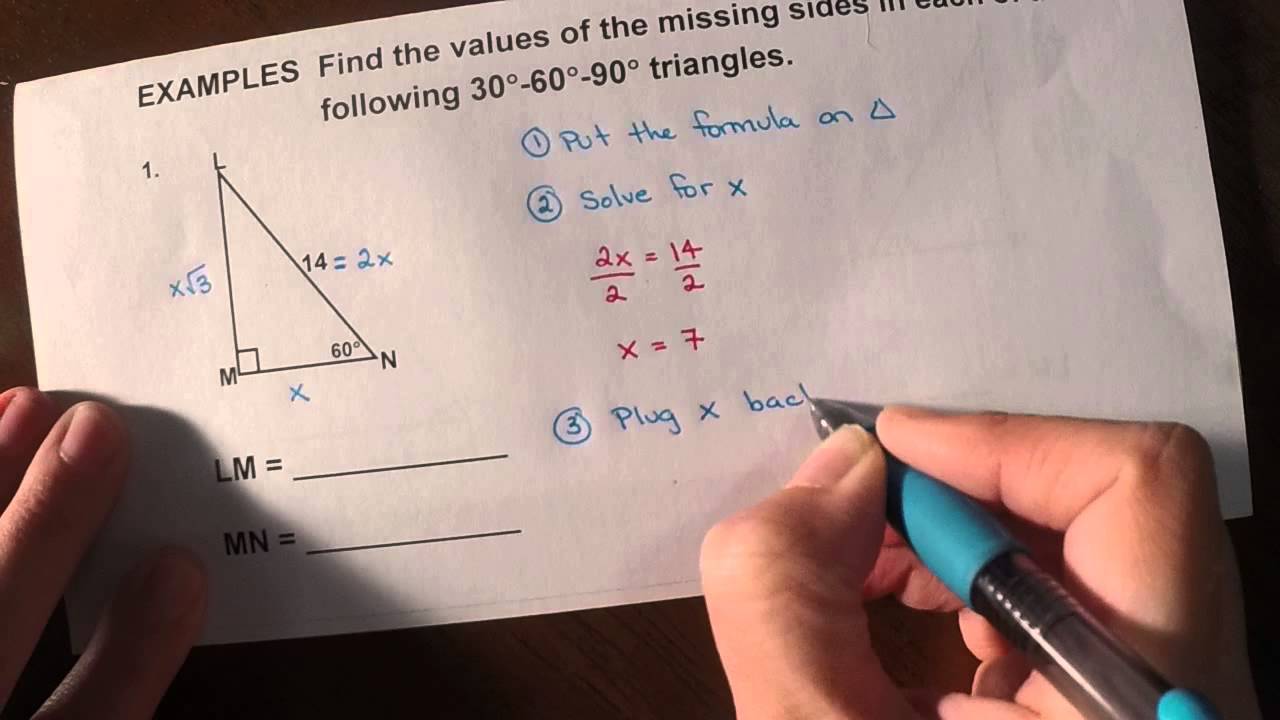



30 60 90 Triangles Youtube




30 60 90 Triangle Theorem Ratio Formula Video




Special Right Triangle Wikipedia
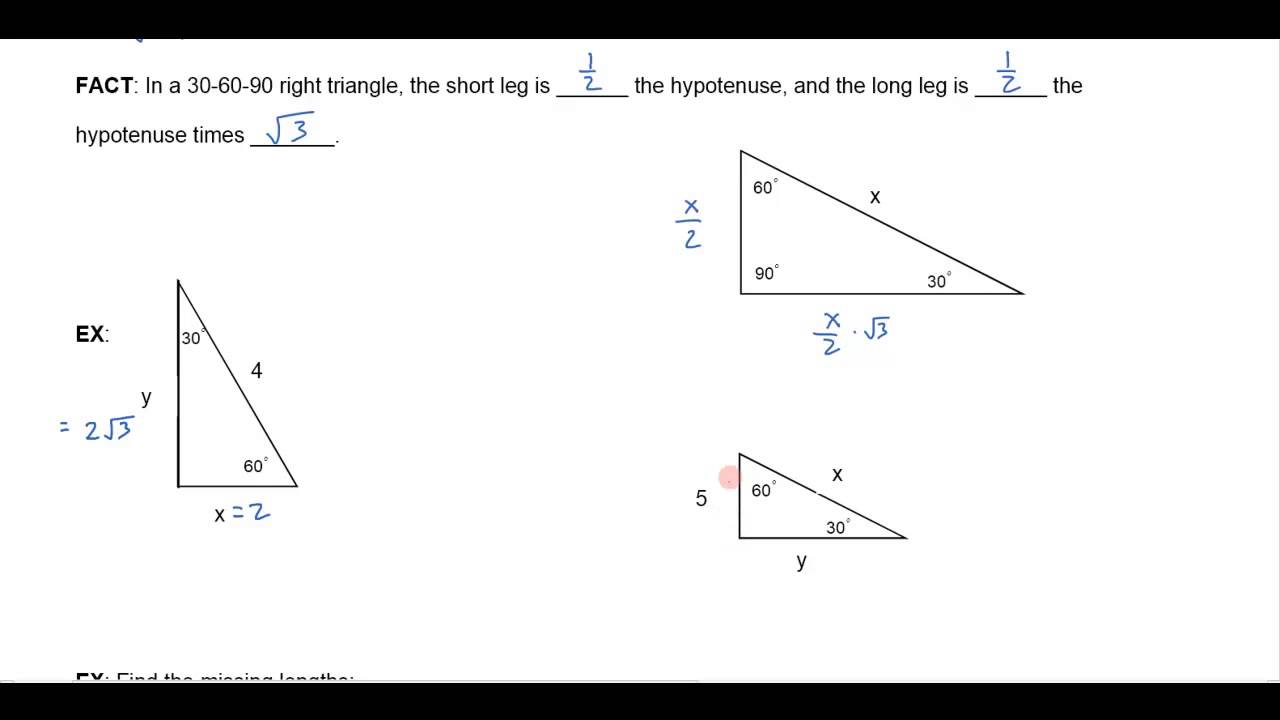



Solving A 30 60 90 Right Triangle Youtube
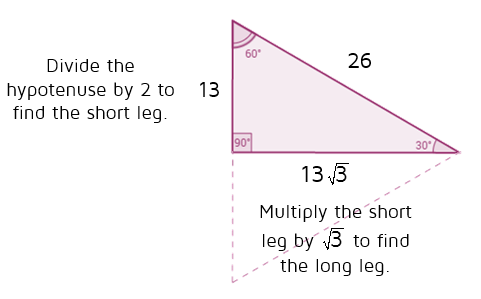



30 60 90 Triangles P4 Kate S Math Lessons
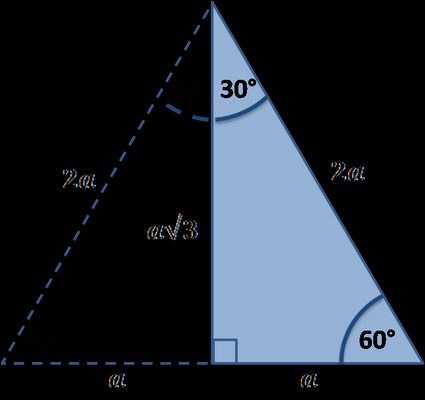



30 60 90 Triangle Calculator Formula Rules




How To Find The Area Of A Right Triangle Basic Geometry




Special Right Triangles Interactive Notebook Page Math Methods Teaching Geometry Teaching Math
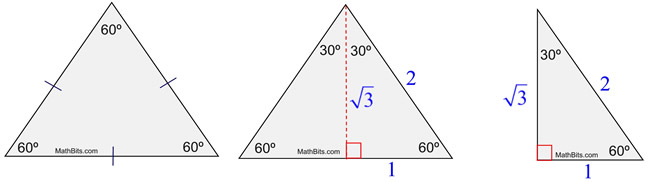



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math



45 45 90 And 30 60 90 Triangles Zona Land Education
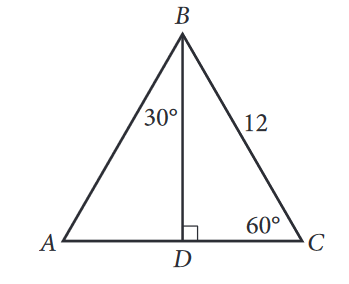



The Complete Guide To The 30 60 90 Triangle



The Easy Guide To The 30 60 90 Triangle
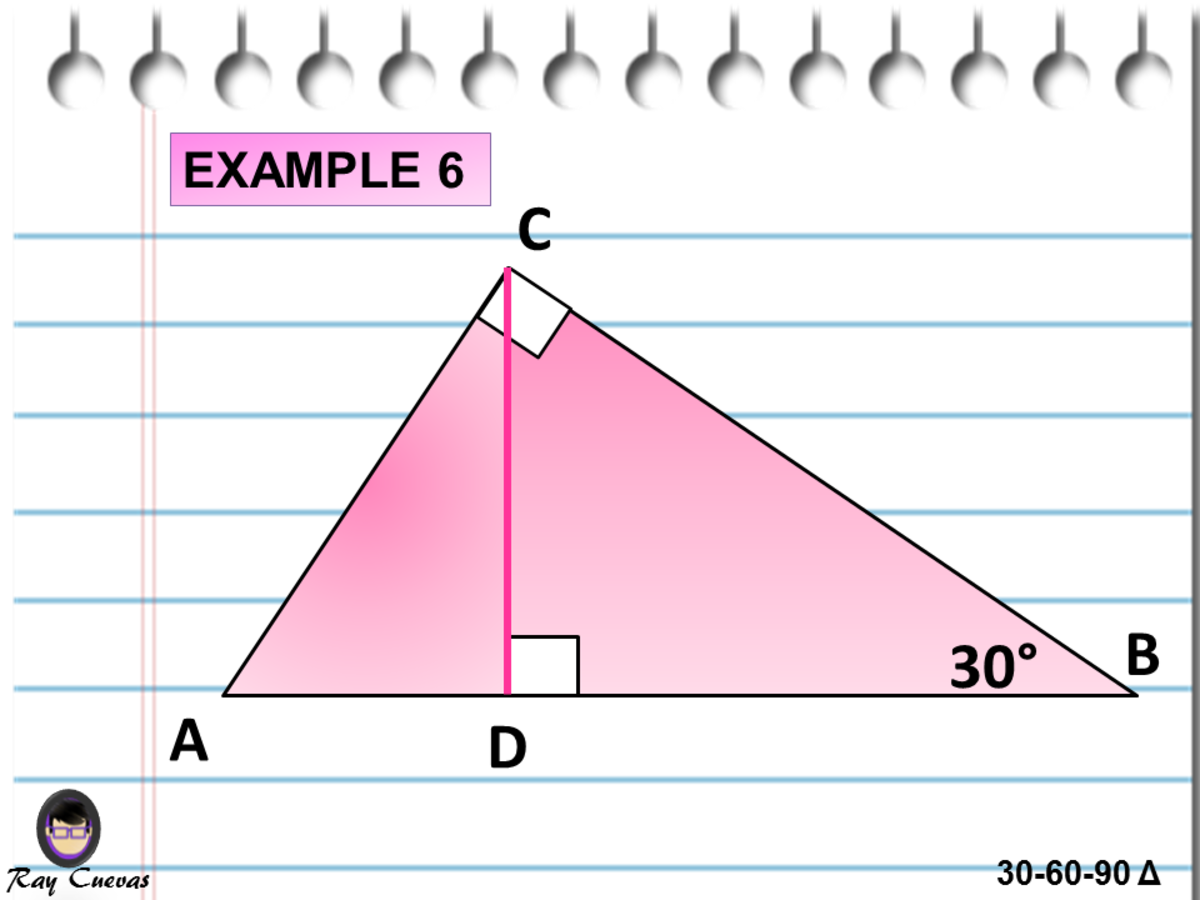



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
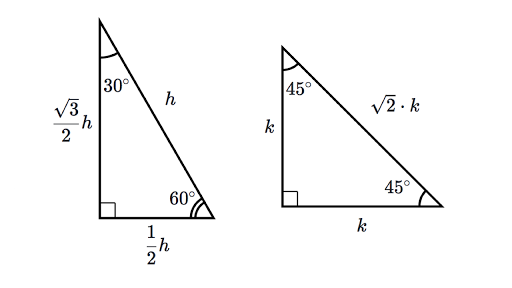



Special Right Triangles Review Article Khan Academy
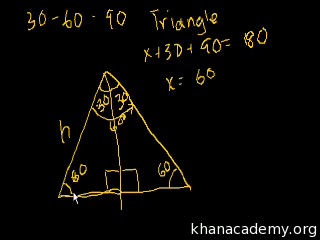



Special Right Triangles Intro Part 2 Video Khan Academy
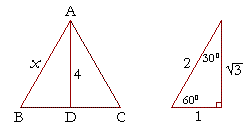



The 30 60 90 Triangle Topics In Trigonometry
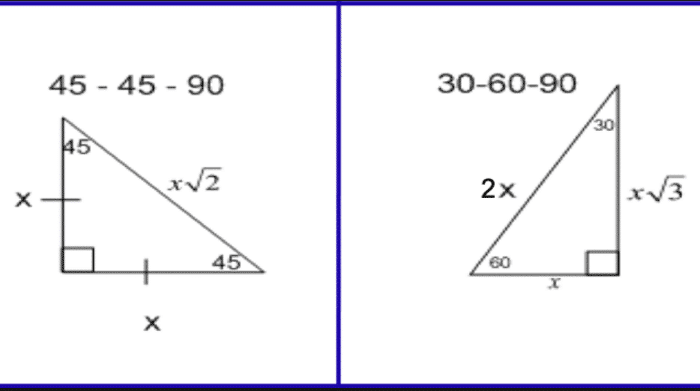



Special Right Triangles Complete Reference Guide The Education




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



1
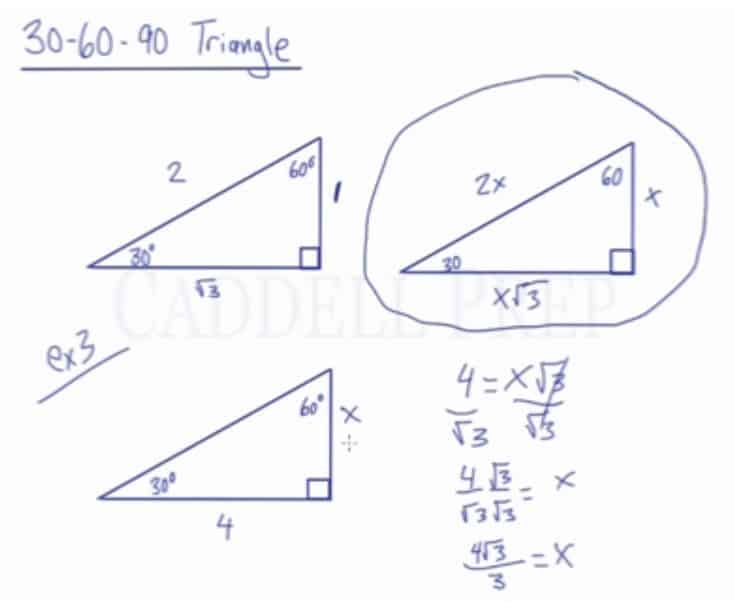



Learn About The 30 60 90 Triangle Caddell Prep Online




30 60 90 Triangle Example Problem Video Khan Academy
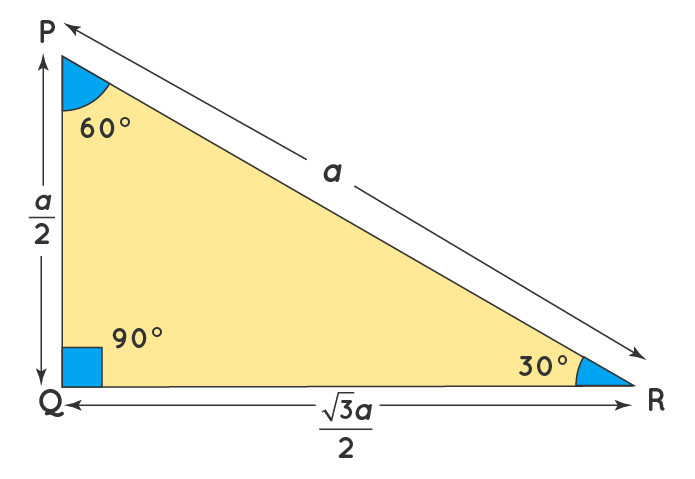



30 60 90 Triangle Definition Theorem Formula Examples
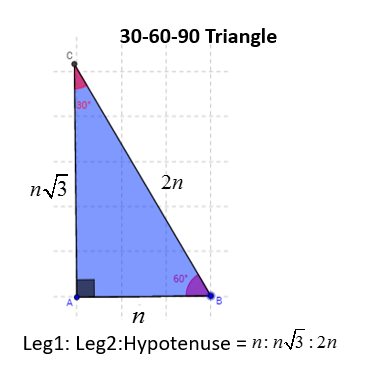



30 60 90 Right Triangles Solutions Examples Videos
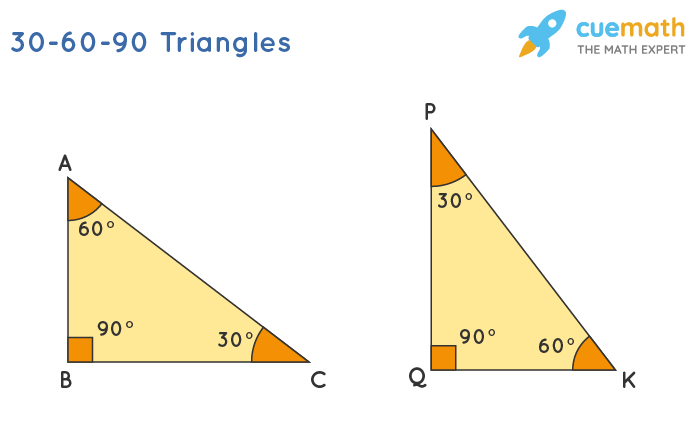



30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Explanation Examples
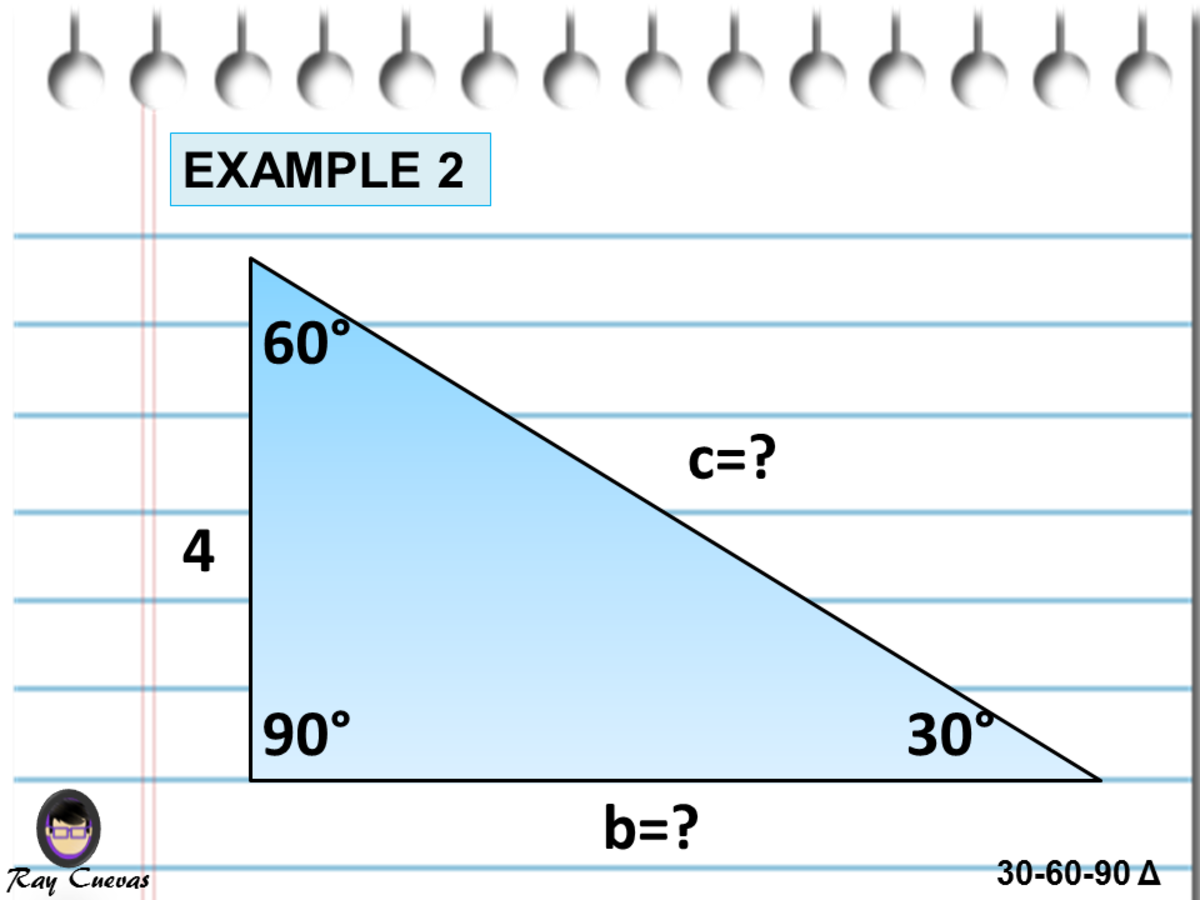



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



0 件のコメント:
コメントを投稿